發現新版本

網站好像有新內容，是否更新？

前言

這是我的第一次CTF
打得很爛writeup也寫得很爛
為了各位的眼睛著想請不要繼續往下看

web

tomorin db

題目觀察

首先點進題目提供的網址 http://chals1.ais3.org:30000/ :

可以看到其中有四個檔案

  • cute.jpg
  • flag
  • is.jpg
  • tomorin.jpg

其中三個是圖片,但flag點進去會跳轉到MyGO!!!!!的聿日箋秋 又在GO

漏洞分析

既然flag文件確實存在,但是/flag路徑做了特殊處理,那我們可以嘗試繞過/flag這個路徑

繞過思路

經過嘗試,我發現如果我們用URL編碼 (%2f) 再加上flag就不會被轉址
所以我在根網址後加上 /%2fflag

我們就可以得到flag

1
AIS3{G01ang_H2v3_a_c0O1_way!!!_Us3ing_C0NN3ct_M3Th07_L0l@T0m0r1n_1s_cute_D0_yo7_L0ve_t0MoRIN?}

Login Screen 1

頁面分析

點進網頁後我們看到了一個登入介面

包含:

  • Username 輸入框
  • Password 輸入框
  • Login 按鈕

注入攻擊


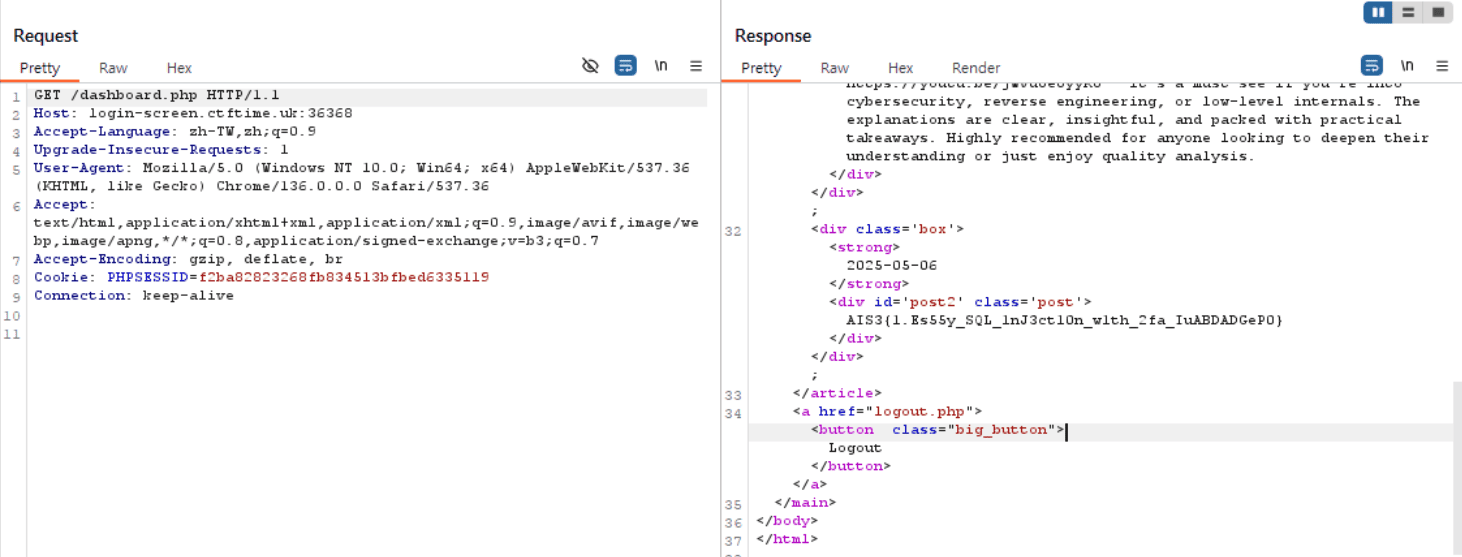
我們就得到FLAG:

1
AIS3{1.Es55y_SQL_1nJ3ct10n_w1th_2fa_IuABDADGeP0}

misc

Ramen CTF

這題是我覺得最有趣的

題目觀察

他給我們了一張圖片

裡面有價值的只有那張發票,我就想到用發票的資訊是不是能查到一些資料

可以得到以下資訊:

  • 平和….
  • MF開頭
  • 2025/04/13的發票
  • 隨機碼 7095
  • 賣方編號 3478592…

接下來用QRcode掃描程式得知:

  • 發票完整號碼 MF16879911
  • 餐點是蝦拉麵

地址尋找

將上面的資料輸入財政部電子發票整合平台


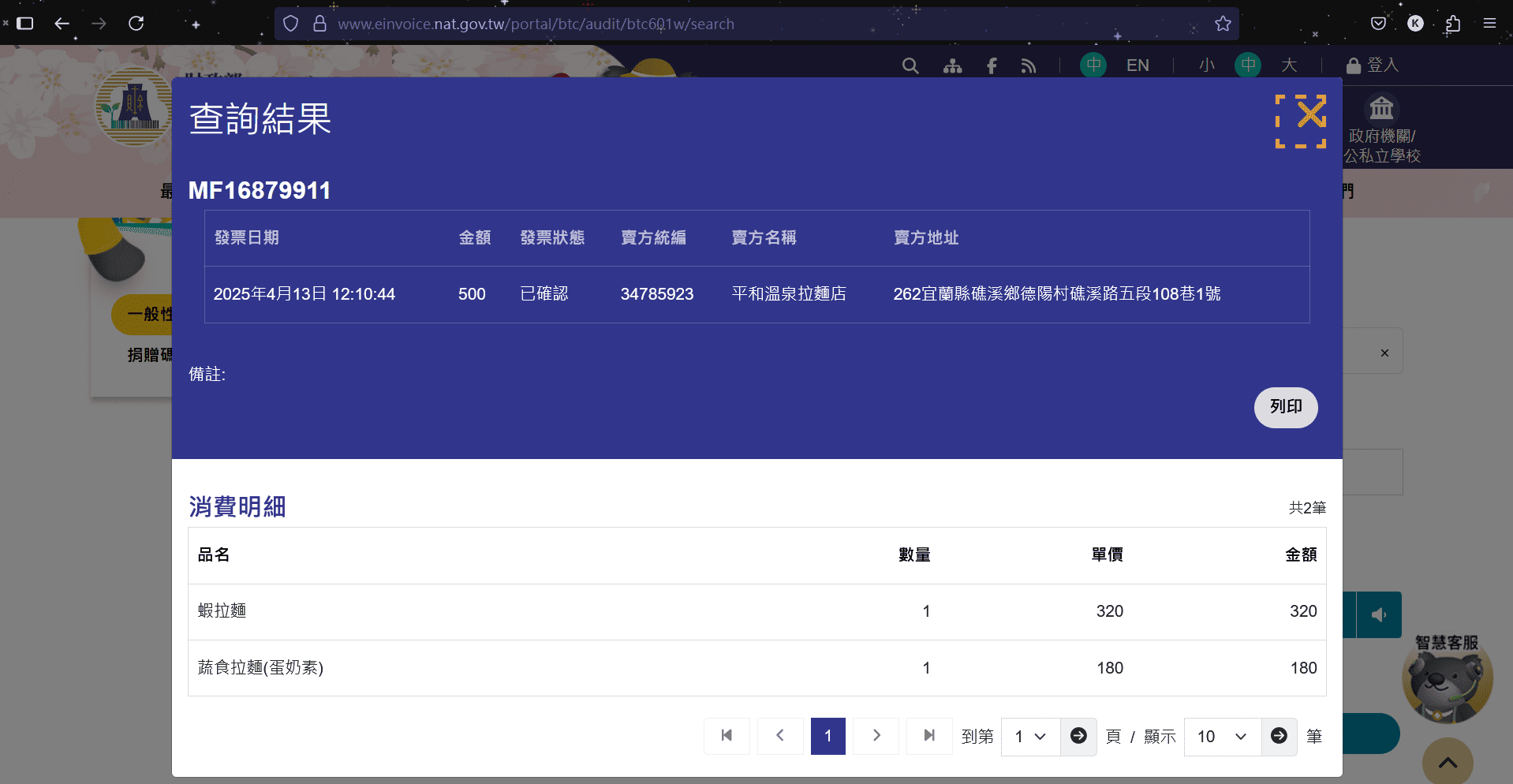
我們就得到了地址,再把地址輸入Google Map
我們可以找到一家 樂山溫泉拉麵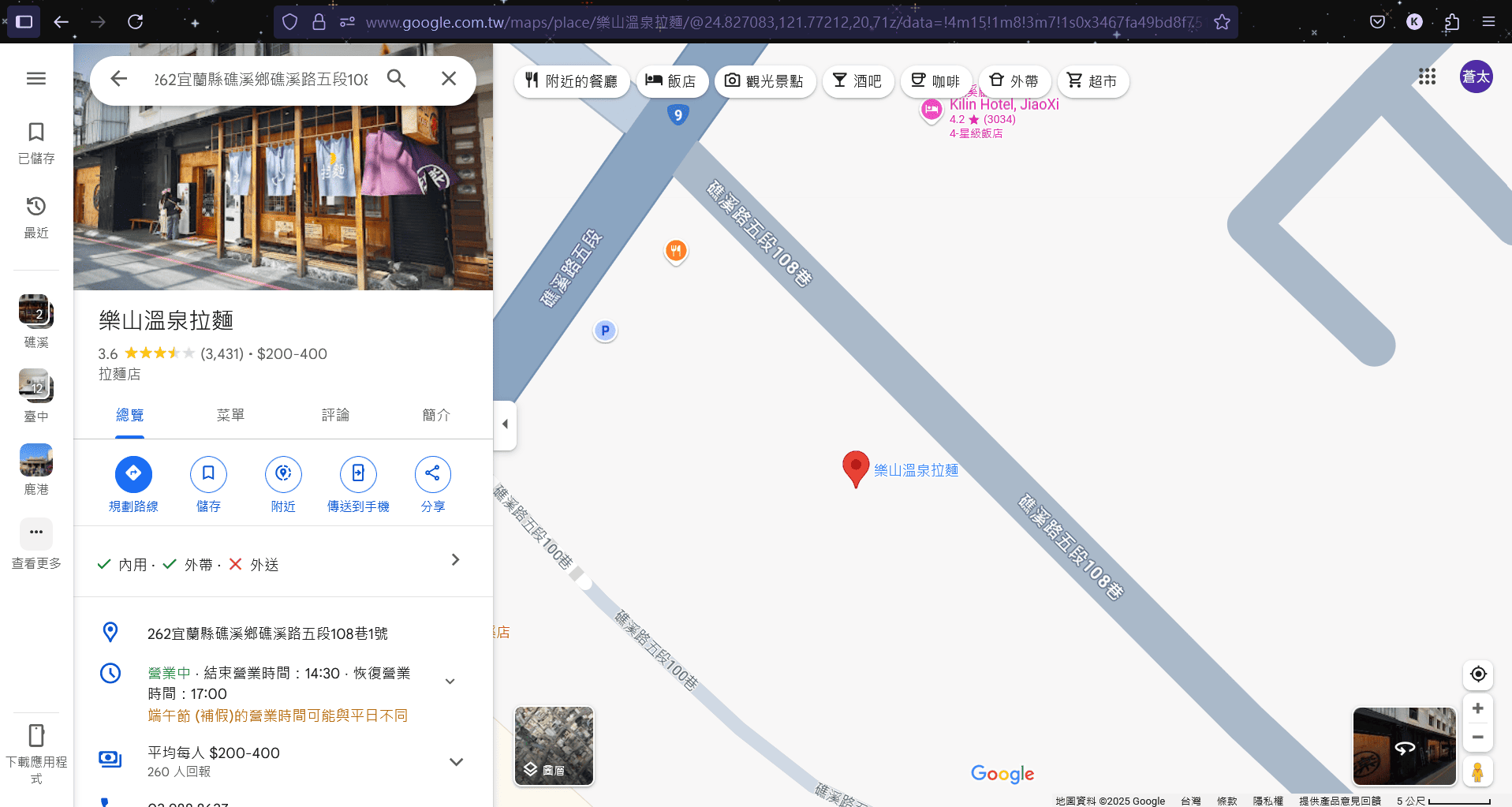

我們就可以得到Flag

1
AIS3{樂山溫泉拉麵:蝦拉麵}

AIS3 Tiny Server - Web / Misc

首先點進題目提供的網址用好token之後
我們會來到 http://chals1.ais3.org:20096/index.html

我就把常見的隱藏路徑都加上去,多次嘗試後發現加//可以叫出文件目錄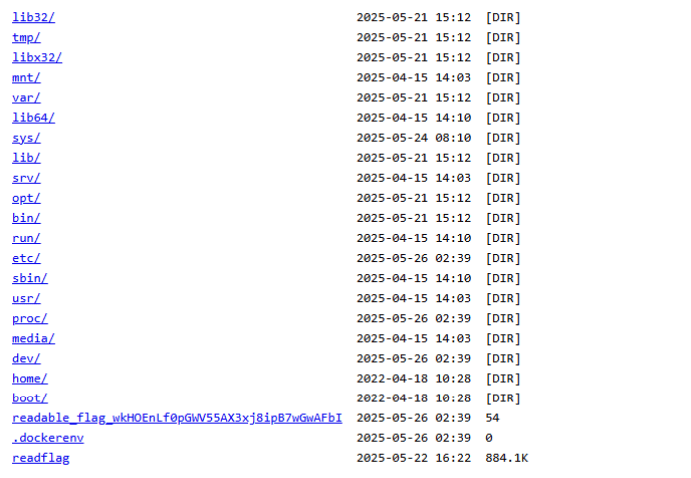

裡面有很多檔案,我就點了檔名有flag的readable_flag_jkO47trw1ctKlOIFC7smx7hivqoCPL8Y

我們就得到了flag:

1
AIS3{tInY_we8_53Rv3R_wi7H_fILe_8R0Ws1nG_AS_@_FeAtURe}

Welcome

我就直接打上去owo

crypto

SlowECDSA

看到題目後，我發現這就是一個經典的LCG攻擊題。ECDSA 的安全性完全依賴於隨機數 k 的不可預測性，如果服務器用 LCG 來生成這些隨機數，那就不難了

收集範本

既然服務器提供 get_example 功能，我就先調用兩次，獲取兩個不同簽名。這樣我就能得到使用連續 LCG 隨機數的簽名對

數學關係

根據Perplexity的資料:
ECDSA 簽名公式是：
$$ s = k^{-1} \times (h + r \times d) \bmod n $$

如果 k₁ 和 k₂ 有線性關係：k₂ = (a × k₁ + c) mod n，那我們就能建一個關於 d 的方程式

求解

從兩個簽名的關係中，可以推導出：
$$ s₂^{-1} \times (h + r₂ \times d) \equiv a \times s₁^{-1} \times (h + r₁ \times d) + c \pmod{n} $$

解這個線性方程就能得到 d。

預測

有了私鑰，我們就能反推出真正的 k₁，然後利用 LCG 的線性性質預測 k₃。

偽造簽名

用預測的 k₃ 和已知的私鑰，為目標消息 “give_me_flag” 生成完全有效的簽名。

攻擊

我叫AI寫了一個 Python 腳本來實現這個攻擊：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
from pwn import *
from hashlib import sha1
from sage.all import *
import re

# 橢圓曲線參數 (secp256k1)
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a_curve = 0
b_curve = 7
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141

# LCG 參數
a = 0x5deece66d
c = 0xb

def get_example_signature(conn):
    """獲取示例簽名"""
    conn.sendline(b'1')
    response = conn.recvuntil(b'Choice: ').decode()
    
    # 解析 r 和 s 值
    r_match = re.search(r'r=0x([0-9a-f]+)', response)
    s_match = re.search(r's=0x([0-9a-f]+)', response)
    
    if r_match and s_match:
        r = int(r_match.group(1), 16)
        s = int(s_match.group(1), 16)
        print(f"[*] Received example: msg='example_msg', r=0x{r:x}, s=0x{s:x}")
        return {'r': r, 's': s}
    else:
        raise ValueError("無法解析簽名")

def solve_for_private_key(sig1, sig2, h, n, a, c):
    """求解私鑰"""
    r1, s1 = sig1['r'], sig1['s']
    r2, s2 = sig2['r'], sig2['s']
    
    # 建立線性同餘方程求解私鑰
    # s2^-1 * (h + r2 * d) ≡ a * s1^-1 * (h + r1 * d) + c (mod n)
    
    s1_inv = pow(s1, -1, n)
    s2_inv = pow(s2, -1, n)
    
    # 重新整理方程式
    # s2_inv * h + s2_inv * r2 * d ≡ a * s1_inv * h + a * s1_inv * r1 * d + c (mod n)
    # (s2_inv * r2 - a * s1_inv * r1) * d ≡ a * s1_inv * h - s2_inv * h + c (mod n)
    
    coeff_d = (s2_inv * r2 - a * s1_inv * r1) % n
    rhs = (a * s1_inv * h - s2_inv * h + c) % n
    
    # 求解 d
    coeff_d_inv = pow(coeff_d, -1, n)
    d = (coeff_d_inv * rhs) % n
    
    return d

def predict_next_k(sk, sig1, h, n, a, c):
    """預測下一個隨機數"""
    r1, s1 = sig1['r'], sig1['s']
    
    # 計算實際的 k1
    s1_inv = pow(s1, -1, n)
    k1_actual = (s1_inv * (h + r1 * sk)) % n
    print(f"[*] Calculated k1_actual: 0x{k1_actual:x}")
    
    # 計算 k2
    k2_actual = (a * k1_actual + c) % n
    
    # 預測 k3
    k3_for_flag = (a * k2_actual + c) % n
    print(f"[*] Predicted k3 for flag signing: 0x{k3_for_flag:x}")
    
    return k3_for_flag

def forge_signature(k, h, sk, G, n):
    """偽造簽名"""
    # 計算 r
    point = k * G
    r = point.xy()[0] % n
    
    # 計算 s
    k_inv = pow(k, -1, n)
    s = (k_inv * (h + r * sk)) % n
    
    return r, s

def main():
    # 連接到服務器
    print("[+] Opening connection to chals1.ais3.org on port 19000: Done")
    conn = remote('chals1.ais3.org', 19000)
    
    # 跳過初始訊息
    conn.recvuntil(b'Choice: ')
    
    # 獲取第一個示例簽名
    print("[*] Getting first example signature...")
    example1 = get_example_signature(conn)
    
    # 獲取第二個示例簽名
    print("[*] Getting second example signature...")
    example2 = get_example_signature(conn)
    
    # 建立橢圓曲線
    E = EllipticCurve(GF(p), [a_curve, b_curve])
    G = E(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
          0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
    
    # 計算 example_msg 的哈希
    h_ex = int.from_bytes(sha1(b"example_msg").digest(), 'big')
    print(f"[*] h_ex (for 'example_msg') = 0x{h_ex:x}")
    
    # 求解私鑰
    sk = solve_for_private_key(example1, example2, h_ex, n, a, c)
    print(f"[+] Recovered private key (sk): 0x{sk:x}")
    
    # 預測下一個隨機數
    k3_predicted = predict_next_k(sk, example1, h_ex, n, a, c)
    
    # 計算 give_me_flag 的哈希
    h_flag = int.from_bytes(sha1(b"give_me_flag").digest(), 'big')
    print(f"[*] h_flag (for 'give_me_flag') = 0x{h_flag:x}")
    
    # 偽造簽名
    r_flag, s_flag = forge_signature(k3_predicted, h_flag, sk, G, n)
    print(f"[+] Forged signature for 'give_me_flag': r=0x{r_flag:x}, s=0x{s_flag:x}")
    
    # 提交偽造的簽名
    print("[*] Sending forged signature to verify...")
    conn.sendline(b'2')
    conn.sendline(hex(r_flag)[2:].encode())
    conn.sendline(hex(s_flag)[2:].encode())
    
    # 接收回應
    print("[*] Server response:")
    response = conn.recvall().decode()
    print(response)
    
    # 關閉連接
    conn.close()

if __name__ == "__main__":
    main()

執行後,我們得到了Flag：

1
AIS3{Aff1n3_nounc3s_c@N_bE_broke_ezily...}

Stream

根據題目提供的python程式,我們看到了這個加密方案的缺陷:
當明文相對於密鑰較小時，XOR 運算的結果主要由密鑰決定
所以我們可以利用數學關係逆向攻擊

思路

現在我們知道加密公式為:

1
encrypted_int = flag_int ⊕ (rand_num²)

當 flag_int 遠小於 rand_num² 時，我們有:

1
encrypted_int ≈ rand_num²

那我們就可以逆推flag了

攻擊

我們先計算近似隨機數:

1
approx_rand_num = math.isqrt(encrypted_int)

再搜索偏移亮:

1
2
for offset in range(-search_width, search_width + 1):
    rand_num_candidate = approx_rand_num + offset

接下來對每個候選隨機數，計算其平方並嘗試解密:

1
2
key_squared = rand_num_candidate ** 2
flag_candidate = encrypted_int ^ key_squared

基本過濾:

1
2
3
4
5
6
7
8
9
# 排除無效結果
if flag_candidate == 0:
    continue

# 檢查長度合理性
num_bits = flag_candidate.bit_length()
byte_len = (num_bits + 7) // 8
if not (5 < byte_len < 80):
    continue

轉換為字串

1
2
3
4
5
6
7
def int_to_bytes(n: int) -> bytes:
    if n == 0:
        return b'\x00'
    byte_length = (n.bit_length() + 7) // 8
    return n.to_bytes(byte_length, 'big')

flag_bytes_candidate = int_to_bytes(flag_candidate)

最後一部,解碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
    try:
        potential_flag = flag_bytes_candidate.decode('ascii')
        
        # 檢查 AIS3 格式
        if (potential_flag.startswith('AIS3{') and 
            potential_flag.endswith('}') and 
            potential_flag.isprintable()):
            
            print(f"[成功] 找到 AIS3 flag，offset: {offset}")
            print(f"候選 rand_num: {hex(rand_num_candidate)}")
            print(f"Flag bytes: {flag_bytes_candidate}")
            print(f"解密結果: {potential_flag}")
            found_flag = True
            break
            
    except UnicodeDecodeError
        continue
    except Exception as e:
        print(f"處理 offset {offset} 時發生錯誤: {e}")

if not found_flag:
    print(f"\n在範圍 [{-search_width}, {search_width}] 內未找到有效 flag")
    print("建議增加 search_width 或檢查加密假設")

運行後我們就拿到了flag:

1
AIS3{no_more_junks...plz}

Hill

系統使用兩個矩陣 A 和 B：

  • 第一個分組：c₀ = A × m₀

  • 後續分組：cᵢ = A × mᵢ + B × mᵢ₋₁

思路

(伺服器只允許一次 input())
我需要一個特殊的輸入序列來同時恢復 A 和 B 矩陣。我想到用標準基向量:
載荷 = [e₀, 0, e₁, 0, e₂, 0, ..., e₇, 0]

當服務器處理這個載荷時：

  • c₀ = A × e₀ 得到 A 的 0
  • c₁ = A × 0 + B × e₀ 得到 B 的 0
  • c₂ = A × e₁ 得到 A 的 1
  • 以此類推…

恢復 A 和 B 後，計算 A 的逆矩陣，然後逆向解密目標 FLAG

攻擊

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
import numpy as np
from sympy import Matrix
from pwn import *
import re

# 設定參數
HOST = 'chals1.ais3.org'
PORT = 18000
n = 8  # 區塊大小和矩陣維度
p_mod = 251  # 模數

def parse_block_line(line):
    """使用正則表達式解析包含8個數字的行"""
    if isinstance(line, bytes):
        line = line.decode().strip()
    else:
        line = line.strip()
    
    # 使用正則表達式提取所有數字
    nums = re.findall(r'\d+', line)
    if len(nums) == 8:
        return np.array([int(x) for x in nums])
    else:
        return None

def inv_mod(matrix, mod):
    """計算矩陣的模逆"""
    A_matrix = Matrix(matrix)
    A_inv = np.array(A_matrix.inv_mod(mod), dtype=int)
    return A_inv

def solve():
    r = remote(HOST, PORT)
    
    try:
        # 1. 先讀取所有初始輸出
        print("[*] Reading all initial output...")
        all_lines = []
        
        try:
            while True:
                line = r.recvline(timeout=2)
                if not line:
                    break
                decoded_line = line.decode().strip()
                all_lines.append(decoded_line)
                print(f"[DEBUG] Received: '{decoded_line}'")
                
                # 如果看到輸入提示就停止
                if any(keyword in decoded_line.lower() for keyword in ['input', 'enter', 'message']):
                    break
        except EOFError:
            print("[DEBUG] EOF reached")
        
        # 2. 從所有行中解析目標 FLAG
        print("[*] Parsing target flag from received lines...")
        C_target_flag = []
        flag_started = False
        
        for line in all_lines:
            print(f"[DEBUG] Processing line: '{line}'")
            
            # 檢查是否開始 flag 區域
            if "encrypted flag" in line.lower():
                flag_started = True
                continue
            
            # 如果遇到輸入提示就停止解析 flag
            if any(keyword in line.lower() for keyword in ['input', 'enter', 'message']):
                break
            
            # 如果在 flag 區域，嘗試解析數字
            if flag_started and line.strip():
                block = parse_block_line(line)
                if block is not None:
                    C_target_flag.append(block)
                    print(f"[DEBUG] Parsed flag block {len(C_target_flag)}: {list(block)}")
        
        print(f"[*] Target flag has {len(C_target_flag)} blocks")
        
        if len(C_target_flag) == 0:
            print("[ERROR] Failed to parse target flag")
            return
        
        # 3. 構造 payload M_payload
        print("[*] Constructing payload...")
        M_payload_blocks = []
        for i in range(n):
            e_i = np.zeros(n, dtype=int)
            e_i[i] = 1
            M_payload_blocks.append(e_i)  # p_{2i} = e_i
            M_payload_blocks.append(np.zeros(n, dtype=int))  # p_{2i+1} = 0
        
        payload_bytes_list = []
        for block in M_payload_blocks:
            payload_bytes_list.extend(list(block))
        final_payload = bytes(payload_bytes_list)
        
        print(f"[DEBUG] Payload length: {len(final_payload)} bytes")
        
        # 4. 發送 payload
        print("[*] Sending payload...")
        r.sendline(final_payload)
        
        # 5. 接收 2n 個密文區塊 (C_response)
        print("[*] Receiving response blocks...")
        C_response = []
        
        try:
            while len(C_response) < 2 * n:
                line = r.recvline(timeout=3)
                if not line:
                    break
                
                decoded_line = line.decode().strip()
                print(f"[DEBUG] Response line: '{decoded_line}'")
                
                if not decoded_line:
                    continue
                
                block = parse_block_line(decoded_line)
                if block is not None:
                    C_response.append(block)
                    print(f"[DEBUG] Received response block {len(C_response)}: {list(block)}")
                    
        except EOFError:
            print("[DEBUG] EOF while receiving response")
        
        if len(C_response) < 2 * n:
            print(f"[ERROR] Expected {2*n} response blocks, got {len(C_response)}")
            return
        
        # 6. 從 C_response 提取 A 和 B
        print("[*] Recovering matrices A and B...")
        A_recovered_cols = []
        B_recovered_cols = []
        
        for i in range(n):
            A_recovered_cols.append(C_response[2*i])
            B_recovered_cols.append(C_response[2*i+1])
        
        A_recovered = np.array(A_recovered_cols).T % p_mod
        B_recovered = np.array(B_recovered_cols).T % p_mod
        
        print("[*] Recovered matrix A:")
        print(A_recovered)
        
        # 7. 計算 A 的模逆
        print("[*] Calculating inverse of A...")
        A_inv = inv_mod(A_recovered, p_mod)
        print("[+] Calculated A_inv successfully")
        
        # 8. 解密 C_target_flag
        print(f"[*] Decrypting {len(C_target_flag)} target flag blocks...")
        decrypted_blocks_list = []
        
        # 解密第一個區塊
        block_0 = (A_inv @ C_target_flag[0]) % p_mod
        decrypted_blocks_list.append(block_0)
        print(f"[DEBUG] Decrypted target flag block 0: {list(block_0)}")
        
        # 迴圈解密後續區塊
        for i in range(1, len(C_target_flag)):
            temp = (C_target_flag[i] - B_recovered @ decrypted_blocks_list[i-1] + p_mod) % p_mod
            block_i = (A_inv @ temp) % p_mod
            decrypted_blocks_list.append(block_i)
            print(f"[DEBUG] Decrypted target flag block {i}: {list(block_i)}")
        
        # 9. 組裝 FLAG 字串
        flag_bytes = b"".join(bytes(list(block_array)) for block_array in decrypted_blocks_list)
        flag_str = flag_bytes.decode('utf-8', errors='ignore').rstrip('\x00')
        
        print(f"[+] Decrypting all target flag blocks.")
        print(f"[+] FLAG: {flag_str}")
        
    except Exception as e:
        print(f"[ERROR] Attack failed: {e}")
        import traceback
        traceback.print_exc()
    finally:
        r.close()

# 主程式入口
if __name__ == "__main__":
    solve()

執行後,我們得到: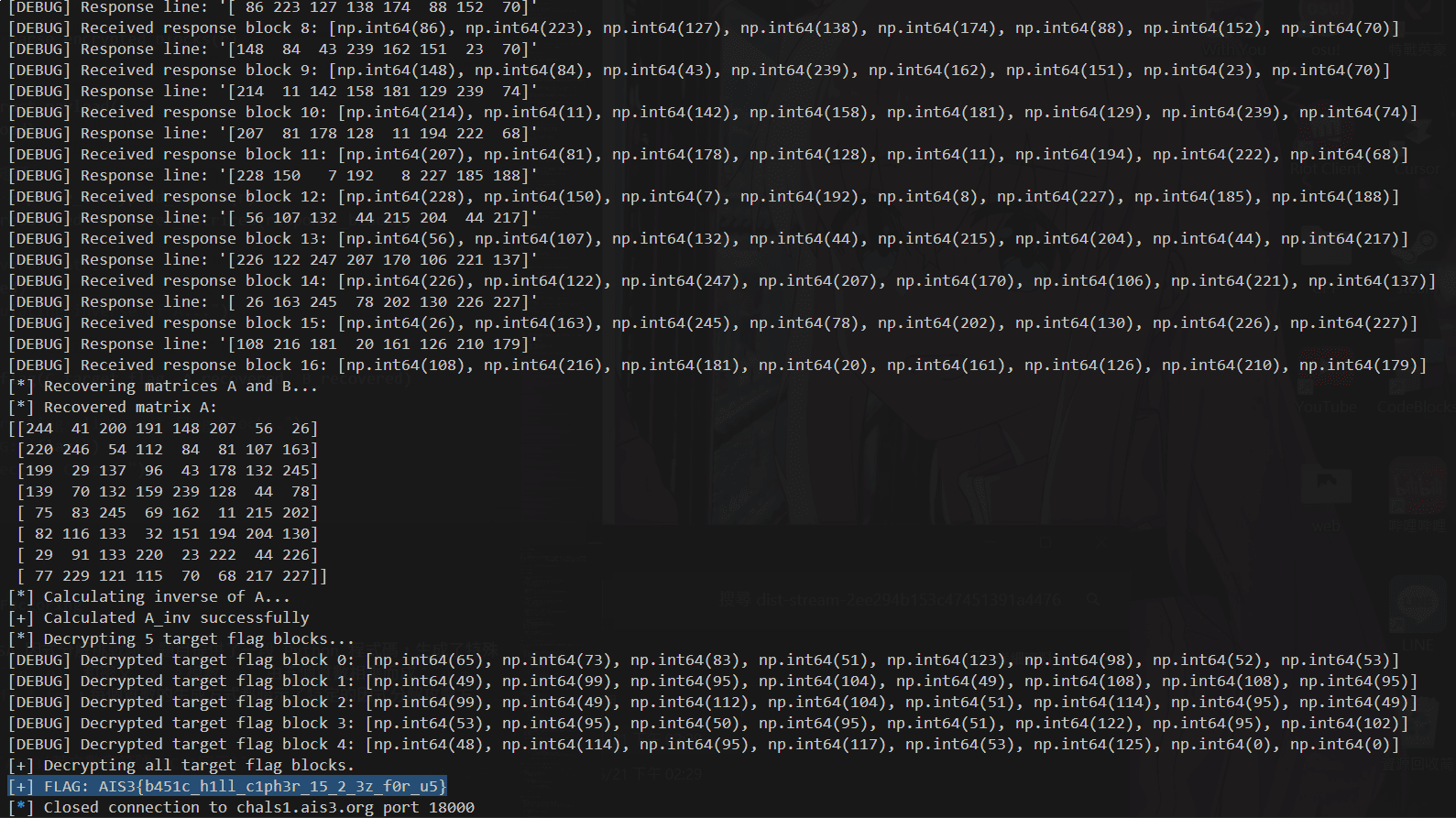

FLAG:
AIS3{b451c_h1ll_c1ph3r_15_2_3z_f0r_u5}

Happy Happy Factoring

這是一個經典的多算法組合攻擊:

  • wi：Williams’ p+1 算法
  • po：Pollard’s p-1 算法
  • fp, fq：Fermat 因式分解法

先用 Pollard’s p-1 找到 po,移除 po² 後用 Williams’ p+1 找到 wi,最後用 Fermat 方法分解剩餘部分

獲得所有因數後計算歐拉函數並解密。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
import gmpy2
from collections import Counter

def read_input(filename="output.txt"):
    with open(filename, "r") as f:
        lines = f.read().strip().splitlines()
        n = int(lines[0].split(" = ")[1])
        e = int(lines[1].split(" = ")[1])
        c = int(lines[2].split(" = ")[1])
        return n, e, c

def generate_prime_list():
    return [p for p in range(3, 5000) if gmpy2.is_prime(p)]

def pollard_p_minus_1(n, prime_list):
    a = gmpy2.mpz(2)
    for _ in range(86):
        a = gmpy2.powmod(a, 2, n)
    for p in prime_list:
        for _ in range(85):
            a = gmpy2.powmod(a, p, n)
    return gmpy2.gcd(a - 1, n)

def extract_factor(gcd_val, n, expected_power=1):
    if gcd_val in [1, n]: return None
    if gmpy2.is_prime(gcd_val): return int(gcd_val)
    temp = gcd_val
    factors = []
    for p in [2] + generate_prime_list():
        while temp % p == 0:
            factors.append(p)
            temp //= p
        if temp == 1:
            break
    if temp > 1 and gmpy2.is_prime(temp): factors.append(int(temp))
    counts = Counter(factors)
    for f, count in counts.items():
        if count >= expected_power and gmpy2.is_prime(f):
            return f
    return None

def lucas_V(k, P, N):
    if k == 0: return 2
    if k == 1: return P
    V0, V1 = 2, P
    for bit in bin(k)[3:]:
        if bit == "0":
            V1 = (V0 * V1 - P) % N
            V0 = (V0 * V0 - 2) % N
        else:
            V0 = (V0 * V1 - P) % N
            V1 = (V1 * V1 - 2) % N
    return V1

def williams_p_plus_1(n, prime_list, P=3):
    V = P
    for _ in range(86):
        V = lucas_V(2, V, n)
    for p in prime_list:
        for _ in range(85):
            V = lucas_V(p, V, n)
    return gmpy2.gcd(V - 2, n)

def fermat(n, max_iter=200_000_000):
    a = gmpy2.isqrt(n) + 1
    for i in range(max_iter):
        b2 = a * a - n
        b = gmpy2.isqrt(b2)
        if b * b == b2:
            return int(a + b), int(a - b)
        if i % 1_000_000 == 0 and i > 0:
            print(f"    [Fermat] 嘗試 {i:,} 次...")
        a += 1
    return None, None

def rsa_decrypt(n, e, c, po, wi, fp, fq):
    phi = po * (po - 1) * (wi - 1) * (fp - 1) * (fq - 1)
    d = gmpy2.invert(e, phi)
    m = gmpy2.powmod(c, d, n)
    flag = int(m).to_bytes((m.bit_length() + 7) // 8, 'big').decode()
    return phi, d, m, flag

def main():
    print("[*] 讀取 RSA 公開參數")
    n, e, c = read_input()
    primes = generate_prime_list()

    print("[*] Step 1: Pollard p-1")
    g = pollard_p_minus_1(n, primes)
    po = extract_factor(g, n, expected_power=2)
    if not po: raise Exception("找不到 po")
    n1 = n // (po * po)

    print("[*] Step 2: Williams p+1 or fallback")
    wi = None
    for base in [3, 5, 7, 11, 13, 17, 19, 23]:
        g = williams_p_plus_1(n1, primes, base)
        candidate = extract_factor(g, n1)
        if candidate and gmpy2.is_prime(candidate):
            wi = candidate
            break
    if not wi:
        print("[!] Williams p+1 失敗，改用 Fermat")
        f1, f2 = fermat(n1)
        if f1 and gmpy2.is_prime(f1):
            wi, n2 = f1, f2
        elif f2 and gmpy2.is_prime(f2):
            wi, n2 = f2, f1
        else:
            raise Exception("找不到 wi")
    else:
        n2 = n1 // wi

    print("[*] Step 3: Fermat 分解 fp, fq")
    fp, fq = fermat(n2)
    if fp < fq:
        fp, fq = fq, fp

    print("[*] Step 4: RSA 解密")
    phi, d, m, flag = rsa_decrypt(n, e, c, po, wi, fp, fq)

    print("\n🎉 解密成功！以下是詳細資訊：")
    print("\n已找到因子：")
    print(f"po = {po}")
    print(f"wi = {wi}")
    print(f"fp = {fp}")
    print(f"fq = {fq}\n")
    print(f"phi_n = {phi}\n")
    print(f"d = {d}")
    print(f"m = {m}")
    print(f"\n🚩 Flag: {flag}")

if __name__ == "__main__":
    main()


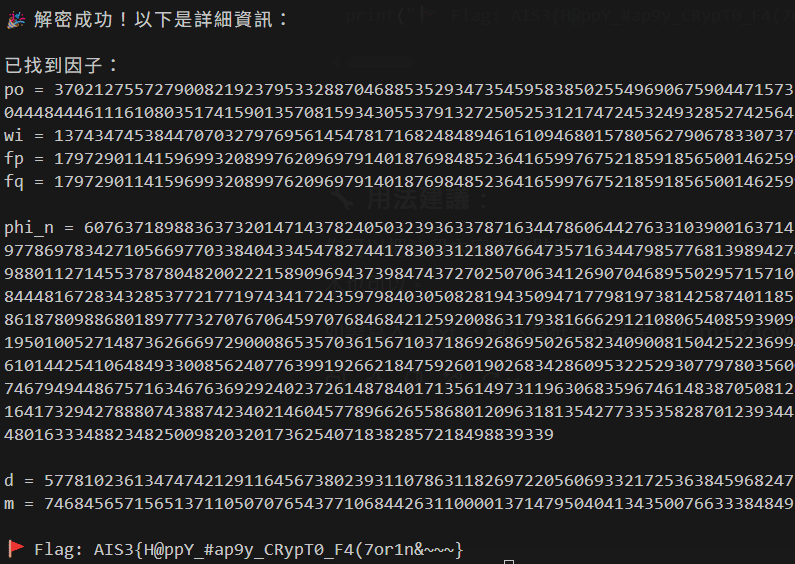
我們就得到了FLAG:
AIS3{H@ppY_#ap9y_CRypT0_F4(7or1n&~~~}

結尾

很高興,你看到這裡眼睛還沒瞎掉
但下面沒東西了,所以我們下次見(?)

說些什麼吧！

waline